Abstract
Conventional medicine treats laboratory tests as "within normal limits" or "abnormal," with no shades of grey in between. This paper explores the utility of using Z-scores to refine the diagnostic criteria for understanding the relationship between TSH, T4, T3, fT4, fT3, and rT3 in the practice of functional and naturopathic medicine.
Conventional Medical View of Reference Ranges
The conventional medical view taught and practiced by allopathic MDs is based on the premise that any lab test result "within the reference range" supports the view that a patient is "normal" and disease-free and, therefore, not a candidate for treatment. On the other hand, any lab test result "outside the reference range" supports the patient being diagnosed with a disease that can be assigned an ICD-10 diagnosis code, and therefore, the patient becomes a candidate for treatment, and the treatment may be subject to third-party payer reimbursement.
This paper will unpack the statistical basis for this view in the following paragraphs. We must discuss certain statistical concepts, including the null hypothesis, statistical significance, confidence intervals, and Boolean logic to do this.
Null hypothesis
The null hypothesis is the starting point of statistical analysis. It states,
In order to make a diagnosis that a patient has a disease, the physician must show that the null hypothesis has a statistically significant probability of being wrong. Note the emphasis on probability rather than proof. Statistics cannot provide proof - only varying degrees of certitude.
There is no effect - there is no problem - prove me wrong.
Rejecting the null hypothesis
In order to diagnose the presence of disease in a patient, statistical evidence must be presented that "it is unlikely" that a healthy patient will present with the particular lab test. In this case, we reject the null hypothesis and accept the alternate hypothesis that there is sufficient statistical certainty that there is an effect, problem, or disease.
Statistical significance
When the statistical certitude that the null hypothesis can be rejected reaches a certain threshold, then it is said that there is statistically significant evidence that the alternative hypothesis (that the patient is diseased) should be accepted. Typically, in medicine, there must be a statistical certitude of at least 95% that the null hypothesis can be rejected for the alternate hypothesis that the patient has an effect, problem, or disease to be accepted. Put another way, there is less than 5% certitude that the patient is "normal." This certitude is often expressed as "having statistical significance at p = 0.05").
Reference range
Various statistical techniques can estimate the reference range (the 95% confidence interval). The most straightforward approach is to collect 1,000 apparently healthy individuals and run the lab test on them. Results are expected to vary according to random chance. If the 1,000 lab values are sorted from lowest to highest, and the 25 lowest and 25 highest values are discarded, then the range of the remaining values will represent the "middle" 95% of the sample. The lowest and highest remaining values represent an estimate of the reference range. This procedure only gives a statistical estimate based on a sample of 1,000 individuals. If the process were repeated with a new group of 1,000 apparently healthy individuals, then a similar but not the same reference range is expected. A less repeatable reference range would be obtained if a smaller sample size were used (e.g., 200 healthy individuals and "trim" off the highest 5 values and the lowest 5 values). A larger sample size would give more repeatable results. The method described here is non-parametric, which means that it does not depend on any assumption of special properties of the data, such as "normal distribution" (see below). In practice, labs may base their reference ranges on statistical techniques that assume the data follows a normal distribution; these reference ranges are only reliable if the statistical assumptions made are valid. Regardless of how the reference range is obtained, it is treated as a uniform (rectangular) distribution in which any lab test value within the reference range equally satisfies the null hypothesis, and any value outside the reference range equally rejects the null hypothesis, which leads to all-or-nothing decision making, as described below.
Boolean logic
Boolean logic is a system of decision-making that is based on "true" and "false" with no intermediate "shades of gray." The conventional medical view taught and practiced by allopathic MDs uses Boolean logic to reason with test results. A given test result is classified as either "in the reference range," which means that it is FALSE that the patient has a problem, or "outside the reference range," which means that it is TRUE that the patient has a diagnosable problem. If the reference range is 0.50 to 4.50, for example, a patient with a test result of 0.51 is treated the same as a patient with a test result of 4.49 - i.e. is "within normal limits" and therefore has no diagnosis of disease. The patient is put into a "box" 4 units wide. Just a smidge to the left or right would cause the patient to fall out of the box and be classified as "abnormally low" or "abnormally high." This view may cause patients near the edges of the box who would benefit from treatment to be told that they are "normal" and to be denied treatment.
Functional Medical View of Reference Ranges
One approach to improving on the conventional medical view as taught and practiced by allopathic MDs is to acknowledge that there are shades of gray between "true" and "false" so that a patient in the above example with lab values of 0.51, 2.5, and 4.4 would be classified as "low-normal," "mid-normal," and "high-normal," respectively. Clinical decision-making can, therefore, be more precise, but the rules for clinical decision-making become more complicated than the conventional approach.
One approach to this problem is introducing the idea of "fuzzy logic." While "fuzzy" may sound like a disdainful term, it represents an acknowledgment that in the real world, decisions must be made with incomplete information of variable reliability. To implement fuzzy-logic decision-making, we can transform the patient's lab value into a Z-score in the same manner as is commonly done for DEXA scan reports of bone density. This Z-score can represent all shades of meaning from "low" (outside the reference range on the left) through "high" (outside the reference range on the right). To understand Z-scores, we must discuss certain statistical concepts, including the central limit theorem, population mean, standard deviation, and Z- transformation.
Central limit theorem
The distribution of many measured values subject to random independent variations tends to follow a "Gaussian," "normal," or "bell-shaped" distribution that approximates a binomial distribution. In particular, if the lab test results of many people are affected by random individual variation, then a graph of the values will be approximately normally distributed, and standard statistical techniques are applicable. In this view, the null hypothesis is most likely to be satisfied at the center of the "hump" of the bell curve and is progressively less likely to be satisfied as the patient's lab value moves left or right toward the "tails" of the bell curve.
This bell-shaped distribution assumption is not a perfect reflection of reality. However, it is a better approximation of reality than the uniform rectangular distribution implied by the conventional approach used by allopathic MDs as described above. As will be discussed below, fuzzy medical decision-making based on the assumption of a normal distribution of test results (e.g., statements like the patient's lab has a Z-score of -1, which means we are about 68% certain that the patient's lab value is abnormal) is expected to be more precise than Boolean medical decision-making using the "in the box/out of the box" approach of assuming a uniform rectangular distribution (which for that same patient we would say "the patient is normal)."
Population mean and standard deviation
Any Gaussian distribution curve can be characterized by the population mean (μ) and the standard deviation (σ). The population mean is the value that represents the top of the hump of the bell curve; the standard deviation is a measure of "how wide" the bell curve is. Without delving into all the mathematics, it can be shown that there is a simple approximate relationship between the reference range described in the conventional medical view and the population mean and standard deviation:
Let L and U represent the lower and upper bounds of the 95% reference range obtained as above (when applied to data that follows an approximately normal distribution).
Then the population mean = μ = (L+U)/2, and the standard deviation = σ = (U-L)/2 .
Z-scores
It is convenient to convert (transform) a patient's lab values into Z-scores.
The following formula converts the measured lab value (denoted V) to its corresponding Z-score (denoted Z):
Z = 2 * (V - μ) / σ
These transformed values have the following convenient properties according to the 68-95 rule:
- Z = 0 means that the patient's lab value is in the middle of the reference range and is most likely normal (the patient is normal from an allopathic perspective);
- Z < -2 means that the patient's lab value is lower than the 95% reference range - reject the null hypothesis at a level of p=0.05 (we are more than 95% certain the patient has a diagnosable disorder from an allopathic perspective);
- Any Z value between -2 and +2 lies within the 95% reference range (within 2 standard deviations of the middle) - accept the null hypothesis at a level of p=0.05 (we are less than 95% certain the patient has a diagnosable disorder, so the patient is considered normal from an allopathic perspective);
- Z > +2 means that the patient's lab value is greater than the 95% reference range - reject the null hypothesis at a level of p=0.05 (we are more than 95% certain the patient has a diagnosable disorder from an allopathic perspective);
- Z-scores are real numbers with a continuum of values representing shades of gray (naturopathic and functional medical perspective)- not just true and false (allopathic medical perspective).
Extending the power of Z-Scores
An advantage of Z-scores is that the reference range is always from -2 to +2, so it is easy to tell where a lab value lies relative to the reference range (low, normal, high). Even more powerful, since Z-scores are continuous, degrees of belief in the null hypothesis can be expressed by intermediate values. If we assume that the test data is approximately normally distributed (which follows from the Central Limit Theorem of statistics), then given the 95% upper and lower bounds of the test data (L and U) and the patient's test value (V), then we can calculate a Z value as follows. For example, consider the case of TSH (reference range = 0.45 to 4.5) and a measured lab value = 3.5, as follows:
Example:
L = 0.5, U = 4.5, and V = 3.5; then
Z = 2 * (V - ?) / ? = 2 * (3.5 - 2.5) / 2 = +1.0
I.e., the patient's lab value is 1 standard deviation higher than the mid-range.Based on the 68-95 rule, we are 68% certain the null hypothesis can be rejected, which means we are 68% certain the patient has a problem that deserves intervention. Do we wait until we are more than 95% certain the patient has a problem, or do we begin mild interventions sooner rather than wait for the patient to cross the line into 95% certainty of abnormality? Where do we draw the line between intervention and watchful waiting?
Assumptions
The following assumptions are more or less accurate - they are not perfect. However, their usefulness is highlighted by a short story:
The story's moral is that the analysis presented here better approximates reality than conventional allopathic medicine, even if imperfect. Therefore, we expect a better, if not perfect, patient response to treatment.
Two hikers in the woods encountered a bear, which began to chase them. As they ran, the first hiker gasped, It is no use - we cannot outrun the bear! To which the second hiker grunted, I do not have to outrun the bear - I only have to outrun you!
Optimality assumption
In the absence of any specific information to the contrary, we assume that the optimal value for a lab value is the center of the reference range, where Z = 0. In other words, the center of "normal" = "optimal." For example, in the thyroid system, a patient is in optimum balance when Z(TSH) = Z(T4) = Z(fT4) = Z(T3) = Z(fT3) = Z(rT3) = 0.
Conversion proportionality assumption
In the absence of any specific information to the contrary, we assume that for a process in which one precursor is converted through one or more steps to a product, if the conversion pathway proceeds at a normal rate, then the Z value of the precursor should be proportional to the Z value of the product. Note that if Z(precursor) > Z(product), it may imply either an abnormally active subsequent step is siphoning off the product or the conversion is impaired. For example, in the thyroid pathway, Z(T4) should equal Z(T3) and also equal Z(rT3) in the case of "normal rate of conversion."
Production proportionality assumption
In the absence of any specific information to the contrary, we assume that if a process in which a control substance causes the production of a product proceeds at a normal rate, the Z value of the control substance should be equal to the Z value of the product. For example, in the thyroid pathway, Z(TSH) should equal Z(T4).
Applications
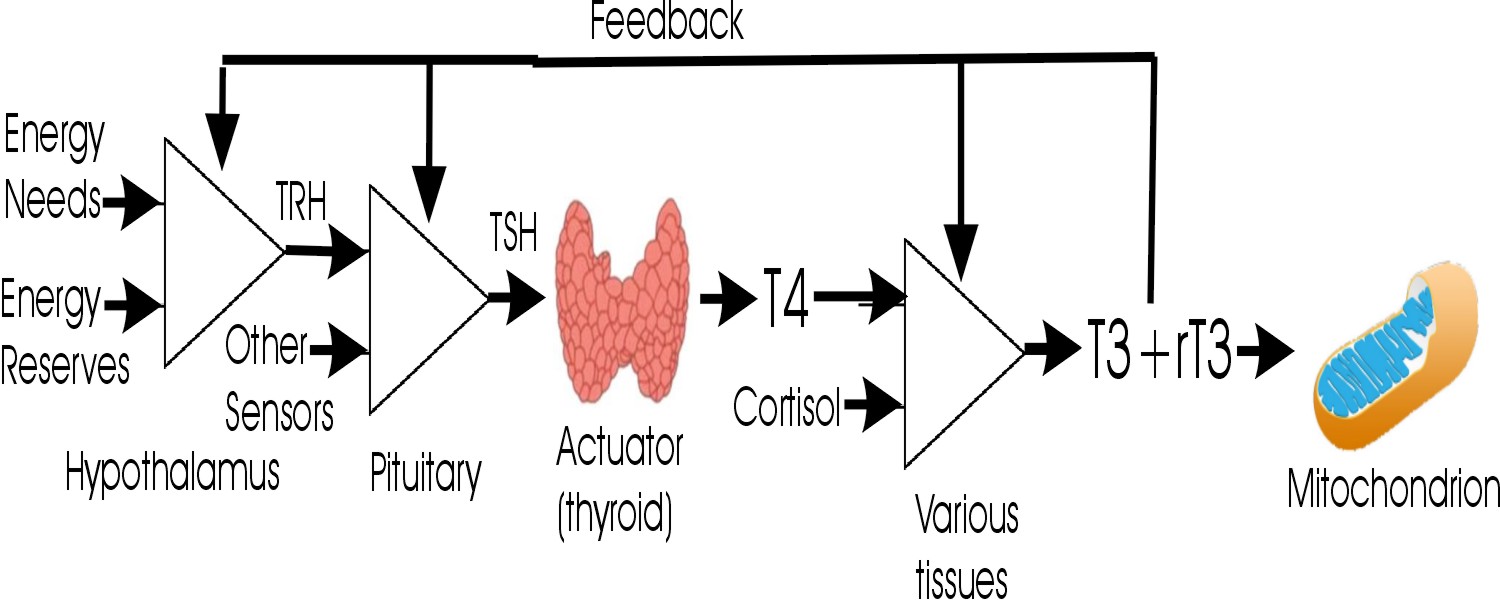
See more details  here
here
Consider the thyroid metabolic pathway below, with Z-values for lab tests as shown:
Z(TSH) = +3
Z(T4) = +1
Z(T3) = -3
Z(rT3) = 0
This patient is hypothyroid, but why?
All three of these issues need to be addressed in the treatment plan.
- Z(TSH) > Z(T4), so we suspect the thyroid gland is underperforming.
- Z(T4) > Z(T3), so we suspect that conversion from T4 to T3 is underperforming.
- Z(T3) < Z(rT3), so we suspect the rT3 pathway dominates rather than the T3 pathway.
Now consider:
Z(TSH) = -1.9
Z(T4) = -1.5
Z(T3) = -1.5
Z(rT3) = +1.9
By conventional standards, this patient is euthyroid but has clinical symptoms. Why?
In this case, we need to reduce rT3, either by supplementing with exogenous T3 or nutritional support for the endogenous conversion of T4 to T3 (e.g., selenium and other micronutrients).
- Z(TSH) < Z(T4), so there is no evidence that the thyroid gland is underperforming - it is not being stimulated.
- Z(T4) = Z(T3), so there is no evidence of a problem converting T4 to T3.
- Z(T3) << Z(rT3), so we suspect that the rT3 pathway is dominating rather than the T3 pathway.
- Z(TSH) << Z(rT3), so we suspect that rT3 is suppressing TSH via negative feedback.
Extension to Fuzzy Logic and Probabilistic Reasoning
Since a Z score of ±1 corresponds to a 68% probability that there is an effect (the null hypothesis fails), and a Z score of ±2 corresponds to a 95% probability that there is an effect (the null hypothesis fails), we can extend our reasoning to propose that if the difference between two Z scores (e.g. Z(TSH) and Z(T4)) equals 1, then there is a 68% probability (P) that the difference is statistically significant. Similarly, if the difference equals 2, there is a 95% probability (P) that the difference is statistically significant.
Boolean logic is used in the conventional medical view of reference ranges to reduce clinical decision-making as to whether it is true or false that each lab value is within the reference range. The functional medical view of reference ranges allows the comparison of non-binary values of different lab parameters using Z-scores. While this is an improvement, it suffers from the limitation that while Z-scores Z(a) and Z(b) can be compared to establish that Z(a) is less than, equal, or greater than Z(b), the significance of the comparison is not defined.
The next step in the development of the theory of thyroid statistics is to develop statistical functions that convert comparisons of Z values into probability functions. For example, if Z(a) = -1 and Z(b) = +0.5, what is the probability that Z(a) < Z(b)? What is the probability that Z(a) = Z(b)? What is the probability that Z(a) > Z(b)? What is the probability that Z(a) is less than the reference range? What is the probability that Z(a) exceeds the reference range? These probabilities are non-zero, but some are much smaller than others.
Based on the assumption that our reference range has a normal distribution, standard statistical calculations should allow all of these functions to be developed using the Excel function NORMSDIST function, which calculates the Standard Normal Cumulative Distribution Function for a supplied value.
What if the Probability Density Curve is not Normal?
Standard statistical methods depend on the assumption that the probability density function (PDF) is a normal bell curve. What if the PDF is distorted by skewness, kurtosis, or other problems? Numerical mathematics can transform these PDFs into normal forms. However, the biggest problem is that raw data is generally unavailable to determine the shape of the distorted PDFs. Presumably, the labs providing the tests have the required data, which they used to establish their reference ranges. However, can we find labs that are willing to share this information?
This is a Draft for Public Comment
Please send comments and constructive feedback to orville2@DrWeyrich.com
Help wanted! (added 01/12/2025)
I need to get access to anonymized thyroid lab data for TSH, F4, T3, freeT4, freeT3, and reverseT3 (or organic acid test data) suitable for determining reference ranges, mean, standard deviation, and evaluating possible deviations from normality. Is there anyone having access to such data that is open to collaborating with me?
Going a step further, it would be even better for me to get access to paired data records containing data for multiple parameters for each (anonymous) individual, possibly including limited demographic data such as sex, age, nutritional sataus, and possibly week of pregnancy in order to evaluate correlations.
Literature Review
Additional reviews will be added as they become available.
 24365659 DOI:
24365659 DOI:  10.1186/1756-6614-6-13 PCMID:
10.1186/1756-6614-6-13 PCMID:  PMC3877984
PMC3877984
Dr. Weyrich has reviewed this paper as part of his literature review to support his ongoing research on statistical methods for diagnosing and treating thyroid conditions, which has previously been reported in [Weyrich2025]. This paper is fascinating because it discusses a statistical methodology for analyzing TSH and free T3 distribution functions. It presents data demonstrating that these distribution functions vary with age, requiring different reference ranges for different ages.
There is controversy regarding the appropriate reference range for thyrotropin (thyroid-stimulating hormone, TSH) and free thyroxine (fT4) in different demographic groups (age and gender).
This study of 1200 "normal" subjects (excluding various abnormalities and confounding factors) found that within the conventional limit of statistical significance (95% confidence interval, p ≤ 0.05), several salient findings were made.
See the paper for a long list of drugs excluded due to their physiological effect on TSH or fF4, for interference with the assays of TSH or fT4, and other exclusion factors.
Major Findings
- TSH increases very significantly with age, while fT4 slightly decreases with age within the whole study population. Dr. Weyrich notes that this suggests that the negative feedback loop between the thyroid and the pituitary is mostly successful in maintaining homeostasis (compensation) of fT4 despite the apparent age-related loss of thyroid function.
- According to the Kolmogorov-Smirnov test, the distribution of TSH values was non-Gaussian. Dr. Weyrich observes that a plot of TSH values in Figure 1 of the paper shows a left-leaning bias with a short left tail (bottom in the figure) and a long right tail (top in the figure).
- The authors report the following distribution data for TSH (modified by Dr. Weyrich; see below):
Age TSH 95% RI Min TSH 25th percentile TSH Median TSH 75th percentile TSH Max TSH 20-49 0.4 - 4.3 0.3 1.1 1.5 2.2 5.8 50-59 0.4 - 4.3 0.4 1.2 1.5 2.6 5.9 60-69 0.4 - 5.8 0.2 1.7 1.75 2.8 8.4 70-79 0.4 - 5.8 0.3 1.7 1.75 3.0 9.5 80+ 0.4 - 6.7 0.2 2.0 2.05 3.5 9.3
 Percentiles for non-Gaussian distributions are
obtained by sorting the data by rank order (lowest TSH value to highest) and determining the value of TSH at which X% of the
data points in rank order are included. By definition, the median value is also the 50% cut-point; for a 95%
reference interval, the lower bound of the reference interval is the 2.5th percentile, and the upper bound of the
reference interval is the 97.5th percentile.
Percentiles for non-Gaussian distributions are
obtained by sorting the data by rank order (lowest TSH value to highest) and determining the value of TSH at which X% of the
data points in rank order are included. By definition, the median value is also the 50% cut-point; for a 95%
reference interval, the lower bound of the reference interval is the 2.5th percentile, and the upper bound of the
reference interval is the 97.5th percentile.
Dr. Weyrich finds it disconcerting that the data reported in the authors' Table 1 show nearly the same value for the 25th percentile TSH and the 50th percentile (median) TSH for ages 60 and above, and he would like to obtain the raw data to confirm the reported results.
Dr. Weyrich suggests that the authors' assumed median TSH reported in Table 1. for the age groups from 60 to 79 should be the average of the male and female values (1.75) rather than the authors' assumption of 1.7.
Likewise, Dr. Weyrich suggests that the authors' assumed median TSH reported in Table 1. for the age group 80+ should be the average of the male and female values (2.05) rather than the authors' assumption of 2.0. - The authors report that the distribution of fT4 was Gaussian, with the following distribution data:
Age fT4 95% RI Min fT4 Mean fT4 (female) Mean fT4 (male) SD (female) SD (male) Max fT4 20-49 0.7 - 1.9 0.7 - 1.7 1.2 1.3 0.03 0.02 1.9 50-59 0.7 - 1.9 0.7 - 1.7 1.2 1.2 0.24 0.25 1.9 60-69 0.7 - 1.7 0.7 - 1.7 1.1 1.1 0.22 0.23 1.8 70-79 0.7 - 1.7 0.7 - 1.7 1.2 1.1 0.24 0.22 1.8 80+ 0.7 - 1.7 0.7 - 1.7 1.1 1.1 0.24 0.23 1.8 - Given the number of subjects analyzed, there was little statistically significant difference between male and female TSH or fT4 distributions for each age group. However, Dr. Weyrich notes that if the sample size were increased, a statistically significant difference may be exposed, which may or may not be clinically significant.
- Dr. Weyrich notes that the reference intervals (ranges) reported above are based on a sample population from the metropolitan area of Rio de Janeiro, Brazil, using a particular brand of test equipment and reagents. These results may not be representative of other demographics or test kits. However, the general patterns reported are likely to be broadly applicable.
- The authors report a "high level of significance" inverse correlation between log10(TSH) and fT4 using the Pearson test:
Age Pearson r R2 20-49 -0.4641 0.1652 50-59 -0.3862 0.1492 60-69 -0.4653 0.2165 70-79 -0.4946 0.2446 80+ -0.3951 0.1561
Dr. Weyrich notes that although this correlation is significant, it accounts for only about half of the trend line, suggesting other significant confounding factors. - Dr. Weyrich laments that all the statistical data above was not reported with more significant figures.
Practical Applications and Questions Regarding TSH and fT4 Abnormal and Optimal Values
- Various researchers have opined that "TSH concentration is the most sensitive test to reliably detect thyroid function abnormalities and is used as the screening test for studying thyroid function because of the inverse log-linear relationship between circulating TSH and FT4 concentrations" [Fontes2013 🕮 ], [Baloch2003 🕮 ], [Benhadi2010 🕮 ].
- The present authors argue that there are no clinically significant differences in TSH and fT4 reference interval distributions based on gender. However, Kratzsch et al. report [statistically significant] lower fT4 in males than in females [Kratzsch2005 🕮 ].
- Other epidemiological studies have also noted that the population's mean TSH levels increase with age [Hollowell2002 🕮 ], [Brochmann1988], [Boucai2011 🕮 ].
- The authors suggest that the observed increase in TSH with advancing age may be "a physiological event" [Atzmon2009 🕮 ], [Surks2010 🕮 ] or may be due to the presence of TSH isoforms with low bioactivity [Estrada2014 🕮 ].
- There is some evidence that low levels of fT4 are associated with better survival in elderly subjects [Vadiveloo2013 🕮 ], [Atzmon2009 🕮 ], [Gussekloo2004 🕮 ], [Beld2005 🕮 ].
- The authors note that in patients having FSH within the reference range, fT4 is associated with atrial fibrillation and lower physical performance [Gammage2007 🕮 ], [Heeringa2008 🕮 ]. This association is especially notable in elderly patients [Gammage2007 🕮 ], [Heeringa2008 🕮 ].
- The authors hypothesize that lower thyroid hormone levels could serve as an adaptive mechanism to prevent catabolism in the elderly [Peeters2009]. Dr. Weyrich wonders if such catabolism results from aging or inadequate nutrition.
- The authors observe that elevated TSH in younger patients, even without decreasing fT4, is related to comorbidities such as dyslipidemia, adverse obstetric events, impact on cognition, quality of life, cardiovascular events, and evolution to clinical hypothyroidism [Biondi2008 🕮 ]. However, the authors further state that there is no evidence that these associations occur in the elderly [Laurberg2011 🕮 ], [Tseng2012 🕮 ]. Dr. Weyrich observes that it is impossible to prove a negative and that "no evidence" suggests "no appropriately designed study with sufficient power has been done."
- The authors observe that "there is a consensus that subjects with TSH concentrations above 10.0mU/L should be treated."
- According to [Garber2012 🕮 ], mild TSH elevations in older individuals, under 10.0mU/L "may not reflect subclinical thyroid dysfunction, but rather be a normal manifestation of aging."
- The authors observe that the TSH reference interval may need to be narrowed for some subpopulations [Baloch2003 🕮 ], [Wartofsky2005 🕮 ], and it may widen with aging [Garber2012 🕮 ].
- The Brave Browser search engine Leo defines "Subclinical hypothyroidism [as] a condition characterized by elevated levels of
thyroid-stimulating hormone (TSH) in the blood, while the levels of free thyroxine (FT4) and
triiodothyronine (T3) remain within the normal range.
This condition is asymptomatic, meaning it does not cause noticeable symptoms.
It is defined biochemically by an increased TSH level combined with" [normal serum levels of free thyroid hormones].
Dr. Weyrich notes that this definition of subclinical hypothyroidism rests on the premise that TSH is a better representation of homeostasis in the HPT axis than fT4 (or fT3). Dr. Weyrich prefers the view that fT3 levels are most clinically relevant, and TSH levels are nothing more than a "control signal" used by the HPT axis to maintain the homeostasis of fT3. Further literature review is necessary to clarify this point.
Details for Geeks
- See regarding the theory of reference values: [Ceriotti2007 🕮 ], [Horowitz2008].
- The
 Kolmogorov-Smirnov Test
is a non-parametric test that can determine whether two sample data sets came from the same probability
distribution. For example, it can compare samples of the non-Gaussian variable TSH from different age groups.
Kolmogorov-Smirnov Test
is a non-parametric test that can determine whether two sample data sets came from the same probability
distribution. For example, it can compare samples of the non-Gaussian variable TSH from different age groups.
According to Leo, in R, the ks.test() function implements this test: ks.test(data, "pnorm", mean = 0, sd = 1).
According to Leo, in Python, the scipy.stats.kstest function implements this test. - The
 Two-tailed Mann-Whitney U Test or Wilcoxon Rank-sum Test
is another non-parametric test that can be used to test whether two sample data sets came from the same probability
distribution.
Two-tailed Mann-Whitney U Test or Wilcoxon Rank-sum Test
is another non-parametric test that can be used to test whether two sample data sets came from the same probability
distribution.
- The
 Kruskal-Wallis Test
is another non-parametric test for determining whether two sample data sets came from the same probability distribution.
Kruskal-Wallis Test
is another non-parametric test for determining whether two sample data sets came from the same probability distribution.
- When comparing two sample populations for the Gaussian-distributed fT4 groups,
 Student's t-Test
(for comparing two groups) or
Student's t-Test
(for comparing two groups) or
 ANOVA can be used (or two or more groups)
ANOVA can be used (or two or more groups)
- Outlying observations can be identified using the
 Dixon Q-test. Dr. Weyrich notes
that this test only applies to small data sets with a Gaussian distribution. See also [Dixon1953].
Dixon Q-test. Dr. Weyrich notes
that this test only applies to small data sets with a Gaussian distribution. See also [Dixon1953].
- Harris and Boyd's method can be used to decide whether it is necessary to use different reference intervals according to gender [Harris1990 🕮 ], [Arderiu1997 🕮 ].
- The authors subjected the TSH data to a log10 transformation to obtain a more Gaussian distribution before correlating
with fT4 data.
This method has been criticized by [Feng2014 🕮 ], [Feng2019 🕮 ], and
 ResearchGate
ResearchGate
- The authors then used the
 two-tailed Pearson test
to correlate the log10(TSH) data with fT4.
A Pearson correlation coefficient of -1 indicates a perfect inverse correlation;
a Pearson correlation coefficient of 0 indicates no correlation;
and a Pearson correlation coefficient of +1 indicates a perfect direct correlation.
Intermediate values suggest the strength of a partial correlation.
two-tailed Pearson test
to correlate the log10(TSH) data with fT4.
A Pearson correlation coefficient of -1 indicates a perfect inverse correlation;
a Pearson correlation coefficient of 0 indicates no correlation;
and a Pearson correlation coefficient of +1 indicates a perfect direct correlation.
Intermediate values suggest the strength of a partial correlation.
References
 9352237
9352237
 19158193 DOI:
19158193 DOI:  10.1210/jc.2008-2325 PCMID:
10.1210/jc.2008-2325 PCMID:  PMC2682478
PMC2682478
 12625976 DOI:
12625976 DOI:  10.1089/105072503321086962
10.1089/105072503321086962  PAYWALL
PAYWALL
 16174720 DOI:
16174720 DOI:  10.1210/jc.2005-0872
10.1210/jc.2005-0872  PAYWALL
PAYWALL
 19926783 DOI:
19926783 DOI:  10.1530/EJE-09-0655
10.1530/EJE-09-0655  PAYWALL
PAYWALL
 17991805 DOI:
17991805 DOI:  10.1210/er.2006-0043
10.1210/er.2006-0043  PAYWALL
PAYWALL
 21058882 DOI:
21058882 DOI:  10.1089/thy.2010.0092 PCMID:
10.1089/thy.2010.0092 PCMID:  PMC3012447
PMC3012447
 17909616 PCMID:
17909616 PCMID:  PMC1994109
PMC1994109
 24073798 DOI:
24073798 DOI:  10.1089/thy.2013.0119 PCMID:
10.1089/thy.2013.0119 PCMID:  PMC3949435
PMC3949435
 25092958 DOI:
25092958 DOI:  10.3969/j.issn.1002-0829.2014.02.009 PCMID:
10.3969/j.issn.1002-0829.2014.02.009 PCMID:  PMC4120293
PMC4120293
 31552393 DOI:
31552393 DOI:  10.1136/gpsych-2019-100146corr1 PCMID:
10.1136/gpsych-2019-100146corr1 PCMID:  PMC6738694
PMC6738694
 17502534 DOI:
17502534 DOI:  10.1001/archinte.167.9.928
10.1001/archinte.167.9.928
 23246686 DOI:
23246686 DOI:  10.4158/EP12280.GL
10.4158/EP12280.GL
Erratum in Endocr Pract. 2013 Jan-Feb;19(1):175
 15572717 DOI:
15572717 DOI:  10.1001/jama.292.21.2591
10.1001/jama.292.21.2591
 2302771
2302771
 19001198 DOI:
19001198 DOI:  10.1001/archinte.168.20.2219
10.1001/archinte.168.20.2219
 15653452 DOI:
15653452 DOI:  10.1515/CCLM.2005.017
10.1515/CCLM.2005.017  PAYWALL
PAYWALL
 11836274 DOI:
11836274 DOI:  10.1210/jcem.87.2.8182
10.1210/jcem.87.2.8182  PAYWALL
PAYWALL
 15961550 DOI:
15961550 DOI:  10.1373/clinchem.2004.047399
10.1373/clinchem.2004.047399  PAYWALL
PAYWALL
 21301488 DOI:
21301488 DOI:  10.1038/nrendo.2011.13
10.1038/nrendo.2011.13  PAYWALL
PAYWALL
 8747831 DOI:
8747831 DOI:  10.1210/edrv-16-6-686
10.1210/edrv-16-6-686  PAYWALL
PAYWALL
 10.1210/jc.2009-2198
10.1210/jc.2009-2198  FULL TEXT
FULL TEXT
 14722150 DOI:
14722150 DOI:  10.1001/jama.291.2.228
10.1001/jama.291.2.228
 19965925 DOI:
19965925 DOI:  10.1210/jc.2009-1845 PCMID:
10.1210/jc.2009-1845 PCMID:  10.1210/jc.2009-1845
10.1210/jc.2009-1845
 22726629 DOI:
22726629 DOI:  10.1016/j.jacc.2012.03.047
10.1016/j.jacc.2012.03.047
 23345094 DOI:
23345094 DOI:  10.1210/jc.2012-3191
10.1210/jc.2012-3191  PAYWALL
PAYWALL
 20016054 DOI:
20016054 DOI:  10.1677/JOE-09-0412
10.1677/JOE-09-0412
 16148345 DOI:
16148345 DOI:  10.1210/jc.2005-0455
10.1210/jc.2005-0455  PAYWALL
PAYWALL
 10.13140/RG.2.2.11927.69281
10.13140/RG.2.2.11927.69281  FULL TEXT
FULL TEXT







